We used soap bubbles to find minimal surface area shapes. These surfaces, given a closed shape, will span the shape using the least area. Using Zometool to make various shapes, we made some fascinating surfaces.

Making Shapes

Zometool is a plastic construction set that is often used for making mathematical structures. It is simple to connect pieces together to make weird shapes, but making a specific shape requires some skill. 

For this project, we wanted to make all the platonic solids and other weird and interesting shapes. After making the shapes, we submerged them in a bubble solution. We used a 1 to 10 ratio of dish soap to water. Below is a photo gallery of some of the surfaces we made.

Gallery

Challenges

We initially planned to make shapes out of metal. We had some 10 gauge brass rods and hoped to cut them to size and then solder them together in the makerspace. However, we ran into some problems. Brass is a very soft material, so when we tried to cut it with the cold saw in the metal shop, the rod bent.

We initially planned to create all of the platonic solids, along with various other weird shapes. However, constructing these wireframes using Zometool was surprisingly challenging. Figuring out how to orient the green rods to produce symmetrical shapes took some trial and error. In the end, we went with a regular tetrahedron, a cube, a squashed version and a stretched version of the cube, a three flap shape, and a nonplanar hexagon.

Math Behind Minimal Surfaces

Minimal surfaces are surfaces that locally minimize their area under a set of given boundary conditions. The simplest way to physically model these surfaces is to blow soap bubbles where the boundary conditions are the plastic rods that function as a wireframe.

These bubbles are minimal surfaces because the bubble takes the simplest shape possible in that it is perfectly smooth without bumps. The flatness of these shapes minimize the surface tension and the area.

More formally, in mathematics, minimal surfaces have roots in Minimal surfaces have roots in differential geometry, variational calculus, mathematical physics, and complex analysis. There have multiple more rigid definitions for minimal surfaces as shown below:

1. Locally: A surface is minimal if every point on the surface has a neighborhood by a simple closed curve, and this neighborhood has the least area among all surfaces with the same boundary.
2. Variational: A surface is minimal if there exists a critical point of the area functional for all compactly supported variations,
3. Differential equations: A surface is minimal if it can be locally expressed as the graph of a solution to a specific partial differential equation.

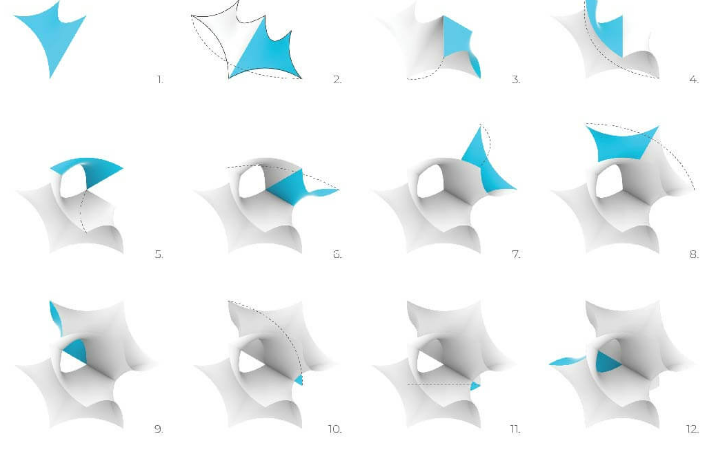
These surfaces can get more complicated as Parametric House shows with this example of the batwing triply periodic minimal surface. These type of structure repeat in three dimensions to create a pattern that extends infinitely in space.

It turns out that proving the existence of these shapes is a surprisingly difficult mathematical problem called the Plateau problem that was only proven in the 1930s. Yet, these soap bubbles seem to do it so effortlessly. You can read more about the history of this problem on this page from FU Berlin.

Future Possibilities

This project could be built upon by trying to model more complex minimizing surfaces such as gyroids, the helicoid, or the batwing above through mediums outside of soap. This could be done analytically using calculus of variations or computationally using an optimization algorithm.