Surface Minimizing Bubbles

The Math Behind Surface Minimizing Bubbles:

As mentioned in the previous blog post bubbles find the minimum surface bounded by a shape. A minimal surface is defined as “having a total curvature equal to zero in every point.” However if air gets trapped in the bubble, the bubble will no longer have a minimal surface (The Shape of Soap Bubbles). Here is an example of a bubble where air interfered with making a minimal surface.

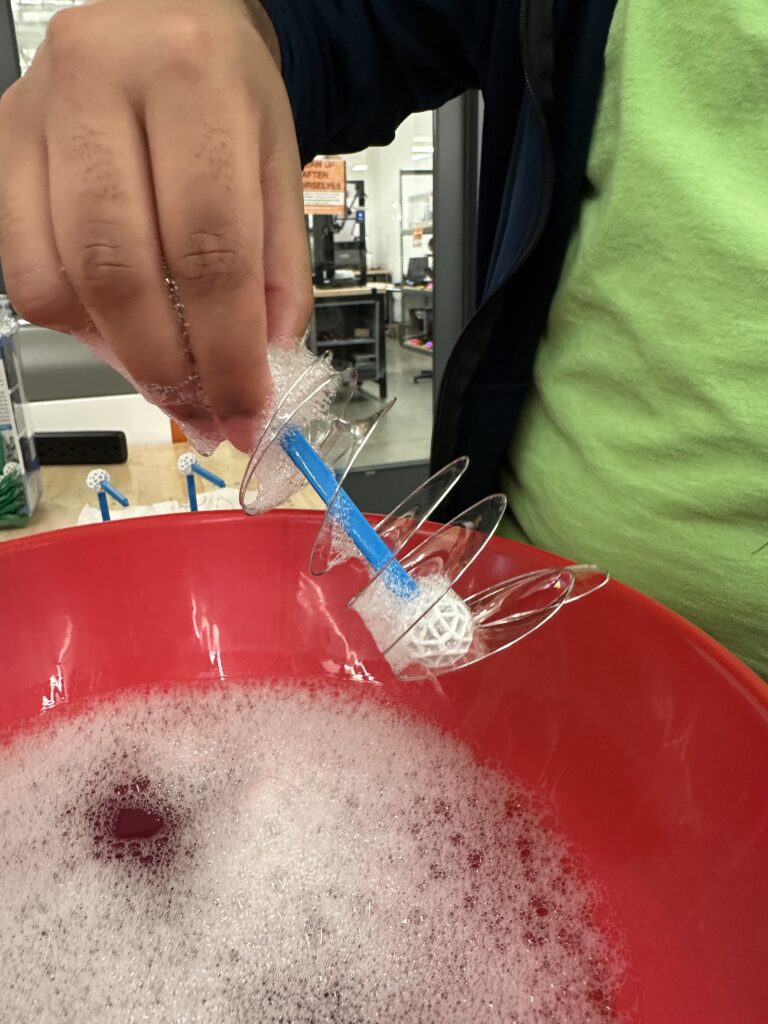
We used this website for inspiration for different shapes to try. For example, we made the spiral shape with a rod through the center. We saw that the distance between the spirals changes how the bubbles form. When the spirals are further apart the bubbles fill in the center of the spiral. In contrast, when the spirals are closer together the bubble connects the sides of the spirals. Here is an image of this happening. 

Here are the additional minimal surface bubbles we made:

Delaney’s Perspective on Teaching How to Make a Hexaflexagon:

I decided to make a much simpler version of a fabric hexaflexagon. Instead of sewing a bunch of triangles together and then making a hexaflexagon we cut out one strip of fabric in the right shape and turned it into a hexaflexagon. This made the process a lot easier and faster. I taught Kaeshav how to use a sewing machine. Threading the sewing machine was still tricky for me but we were able to figure it out. 

Delaney’s Perspective on Learning about Surface Minimizing Bubbles:

It was exciting to learn how to make bubbles this way. I didn’t realize that bubbles naturally find the minimum surface area. This was exciting to learn and to see how it played out with different shapes. 

Hexaflexagons

To make the hexaflexagon, we decided to use one piece of fabric to make it easier.

The first step of making a hexaflexagon is cutting the fabric to size. We used a helpful paper guide to help us correctly cut the fabric.

After cutting the fabric to size, we sewed the two long edges of the fabric together to get a tube.

We then inverted the tube so that the pattern is on the outside. Then, we attempted to fold the hexaflexagon into a triangle as shown by the paper model. Then, we would iron it to keep the edges folded in.

However, the hexaflexagon did not fold up perfectly evenly, indicating that there was some error that was unaccounted for when cutting and sewing. Nevertheless, we still closed it up and ended with a very striking pink zerbra hexaflexagon.

There are also more complex hexaflexagons out there. Some examples are shown in Martin Gardner’s Hexaflexagons and other Mathematical Diversions [1]. We made a trihexaflexagon which can bring three faces into view. You could also make a hexahexaflexagon which has six faces that can be brought into view. There is also a higher dimensional version called a flexatube. This tube can be turned inside out using specific folds [2].

Refrences:
[1] Garder, Martin Hexaflexagons and other Mathematical Diversions.  University of Chicago Press (1998)
[2] Weisstein, Eric W. “Flexatube.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/Flexatube.html