For our project we represented different probability distributions using beaded jewelry. We wrote some code to generate bracelet layouts for us, so all we needed to do was to actually assemble the bracelets.

We initially made a test bracelet together. We tied elastic string in a knot.

We then decided to try making more sophisticated bracelets using metal clasps. However, this proved to be more challenging than anticipated. Most of us were new to bracelet making, so we were not expecting the procedure of closing the bracelet to provide any difficulties. Due to this, we dropped almost finished bracelets multiple times.

We ended up working in parallel where we each focused on representing a different probability distribution and used different techniques to make jewelry. We helped each other throughout the process as we each learned new things.

Mathus represented the Poisson distribution, which counts the number of times an event occurs in a certain period of time. The probability mass function (PMF) is shown below:

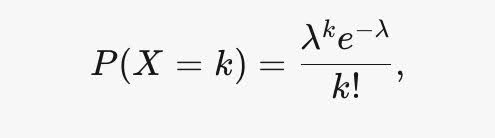
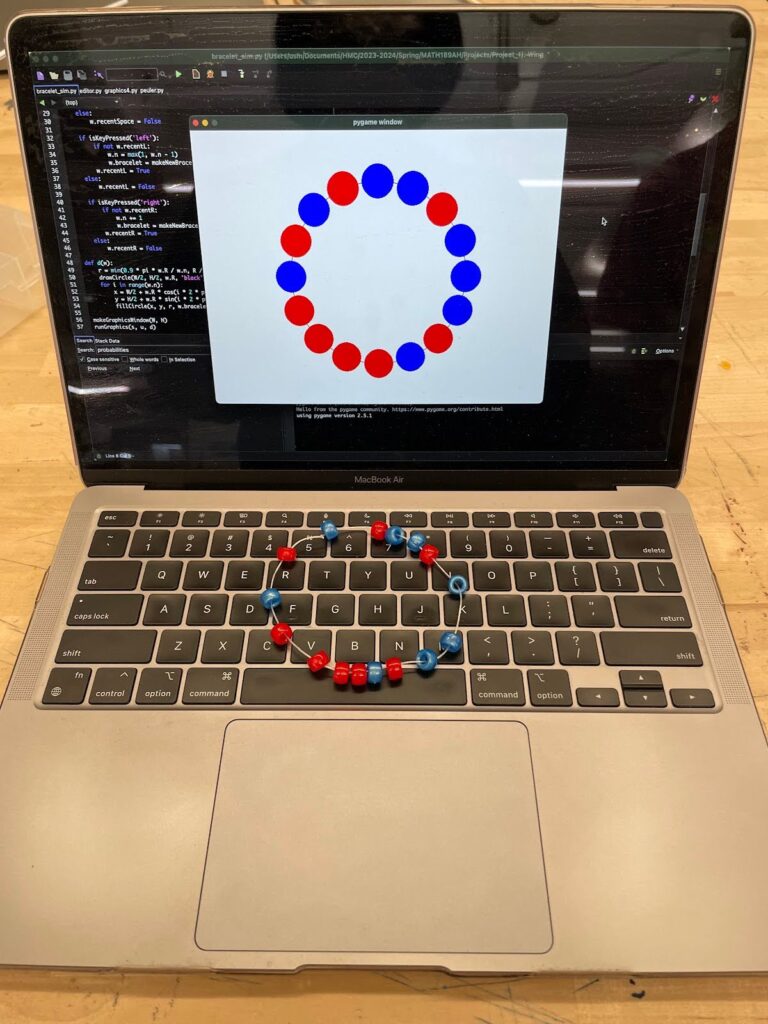
In the PMF, k is the observed number of events and λ is the expected number of events in the time interval. To generate the bracelet layout, I used λ = 2 and took 24 samples. I then converted each sample to a color corresponding to its number. At first, I tried to follow the wikiHow instructions for a multistranded bracelet and even got to the last step, but unfortunately dropped everything. I also struggled to close the bracelet off, as I did not have enough string to do so. Eventually I swapped to some sort of technique dubbed the “lizard tail” where I would run a thread through pairs of beads in both directions. After threading all 24 colored beads, I could then tie the large amounts of excess thread together, producing the below necklace.

Ashrit focused on the Geometric distribution, which is a discrete probability distribution that can be used to find the probability of getting the first success on a certain trial. Below is the PMF of the Geometric Distribution:

While creating the distribution bracelets for the Geometric distribution, we generated both a single-strand bracelet and a double stranded bracelet. We found a useful wikiHow on to generate these types of bracelets and followed along. We ran into a few problems while doing so, as it was hard to tie the ends together as they would often become narrow and multistranded. It would also be hard to keep track of where the ends were. The single-stranded bracelet did not come together as properly as we hoped, as we followed a computer generated pattern for the Geometric, yet, we came across problems when implementing, where the beads exploded off our bracelet multiple times causing us to start over or us not being able to tie together the opposite ends.

However, the double-stranded bracelet came together much better, as we took longer pieces of strings, and were more creative in ways to keep it together. I took short rubber stubs and connected them to the end of each string to prevent the beads from coming out, and used Delaney’s suggestion of double knotting a piece of circular metal to the end of the strings to keep them from untangling.

Delaney focused on the binomial distribution, which counts the number of successes in a number of independent trials. Below is the PMF of the binomial distribution:

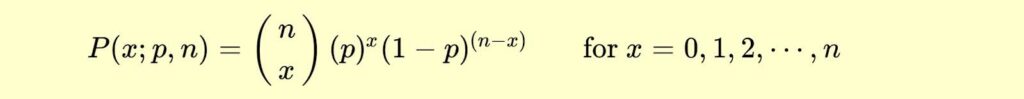
In the PMF, p is the probability of a success and n is the number of trials. After failing to follow the wikiHow article, we decided to start with a metal ring double knotted in the middle of a long strand of fishing wire. Then threaded the computer generated beads onto both strands of the wire. At the end, another metal ring was double knotted onto the strand and the excess wire was cut off. The wire ended up being cut too short, which caused the knots to come undone and the strand to explode. We repeated this process, leaving longer tails of string after the knot. We attached the two strands together, using more metal rings and metal clasps. This resulted in a multi strand bracelet. Each strand represents one binomial trial. The pink represents a success, while the blues represent a failure. The bracelet demonstrates how different binomial trials with the same p value can have different results.

These bracelets are colorful ways to display probability distributions, while also teaching us about jewelry making methods in the process.