For this project, I wanted to create Burr Puzzle using wood. The biggest creative deviation I took is using approximately half the thickness a traditional Burr puzzle would to scale down the puzzle.

At first glance, a burr puzzle looks like a simple arrangement of wooden pieces, each with notches and slots. However, the goal of a Burr puzzle is to interlock the pieces in a manner where disassembling the puzzle becomes a challenging task. The puzzle on the left is a picture of the most common type of burr puzzle which has six pieces where three sets of two rods intersect each other. However, this is not the only type of burr puzzle, the one on the right is one with six pieces but sets of only one rod and is made of stone!

the Math behind Burr Puzzles

Burr puzzles delve into multiple mathematical concepts including geometry, group theory, topology, combinatorics, and graph theory. The intuition behind geometry and topology is more straightforward given the complexities in trying to model the rotations and notches of the actual structure of the puzzle.

Given the breadth of these concepts, I decided to focus on group theory and combinatorics. Remember that the key properties of a group are closure, identity, inverse, and associativity. Each puzzle has various symmetries whether those be rotations, reflections, or combinations of the two. These properties ensure that any valid combination of transformations will yield another valid configuration of the puzzle. Other implications include that for every transformation, there exists a corresponding transformation that can reverse its effect. Lastly, the sequence of operations performed can be rearranged without altering the final configuration of the puzzle.

Combinatorics helps quantify the numerous possible configurations a burr puzzle can have. Counting principles and permutations enable us to systematically enumerate all of these configurations due to the puzzle’s symmetry.

This can even be connected to graph theory where puzzle pieces are modeled as vertices and their interlocking relationships are modeled as edges. Combinatorial graph theory, using concepts like spanning trees and cycle detection, would then look at the connectivity of these graphs to identify potential solution paths.

Prototype 1: Wood

Because I wanted to cut down on the scale of the burr puzzle, I used a slimmer, longer piece of wood:

Before cutting the wood, I planned the deign of the puzzle to determine how each piece should be cut. Given each puzzle is symmetric, I first started by separating this wood into six equal sized pieces using a table saw to get the following:

I then made Next I attempted to use the band saw and table saw to try and cut the individual pieces. I measured out how each piece should be cut.

Because I had chosen a smaller depth, my margin of error was considerably lower. My cuts needed to be more precise because if I went too far, I would have split the wood in half which I did multiple times. After multiple attempts, I was able to create something that vaguely looked like a burr puzzle piece but the notches were nowhere near as precise as they needed to be.

After a lot of cuts I got one piece to look like the above picture but the edges were still rough. I attempted to chisel the nooks in between but due to my lack of experience wit woodworking, I was not able to chisel anything precisely. I either knocked off too much wood or nothing at all.

By the end of all of this, I learned that woodworking is very hard – much harder than I had expected it to be and so I took to 3D printing to see if I could make that work.

Prototype 2: 3D Printing

Once I abandoned the wood, I started to model the burr puzzle using Autodesk. Thankfully, I had some previous experience with 3D modeling software and there were lots of guides online.

I found a mold for a burr puzzle online and modified it to be slimmer like I initially intended. These were the pieces from three different angles:

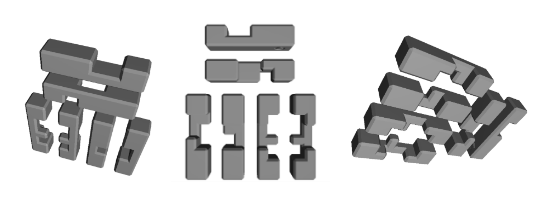
I then went to 3D print them out but haven’t had a chance to pick them up yet. I think I might also try printing them on the nylon powder printer if these initial prints don’t go well.

Future Project Improvements

I still want to try creating a scaled down burr puzzle but I think I’d first need to do some easier woodworking projects first. That way I can get comfortable with the tools before attempting something this challenging.

I think something else cool would be to paint the burr puzzles using cool geometric designs or even wallpaper groups (as my other classmates did). I think it would be cool to try and create different patterns depending on how the pieces get interlocked – especially because I haven’t really seen that with existing burr puzzles.