Representing the Fibonacci Spiral in 3D

In this project, Ambika and Ashrit worked on finding a physical representation of the Fibonacci sequence. 

We all know the Fibonacci sequence as series of numbers where each number is the sum of the two previous numbers as shown below: 

1 1 2 3 5 8 13 21 34 . .. 

However, you may also have seen the representation of it as a spiral: 

For our project, we wanted to focus on this spiral concept as it can represent the ratio between two quantities where the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. Each rotation along this path would be 137.5 degrees.

To approach this we had a few ideas of machines or tools we wanted to use to represent the sequence:

Laser Cutting 

Knitting 

3D Printing 

Powder Printing

We were inspired by the different structures Prof. Kagey made in the powder printer and wanted to also follow a similar design. Neither of us had used the powder printer before and were excited to learn the new technology. 

To do this we need to generate stl files, and there was no better way of doing this than revisiting a technology we learned in class previously: openSCAD. 

Shown below is an example of the Fibonacci spiral and Golden Ratio being used to show the layering of a cube: 

Here is an overview of the code: 

Variables: 

WALL_THICKNESS: Specifies the thickness of the walls of the structure

SIZE: Defines the initial size of the structure.

STEPS: Determines the number of steps or layers in the structure.

TOTAL_ROTATION: Specifies the total rotation angle of the structure. (this would be 137.5 for us to represent the golden spiral) 

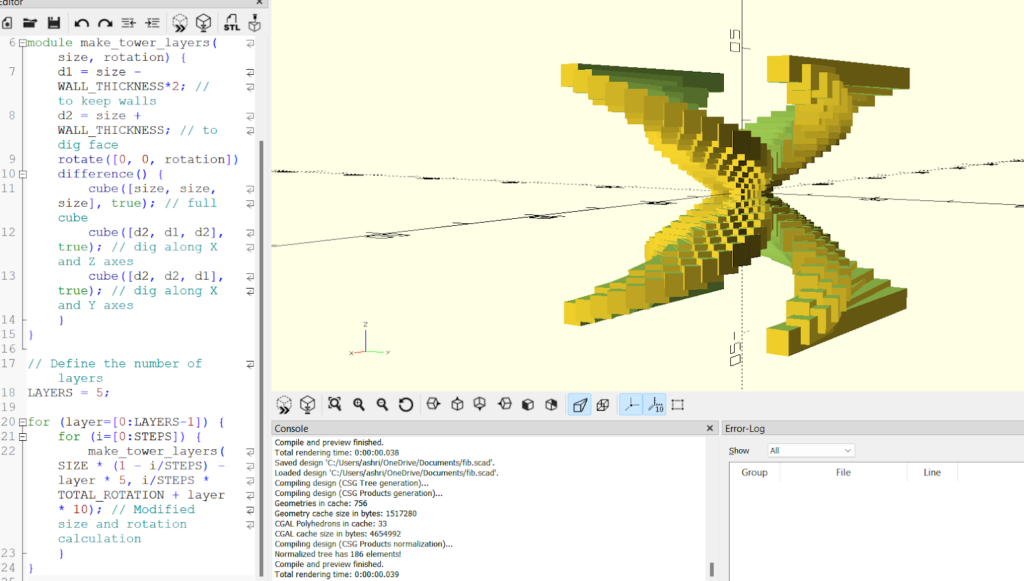
There were two modules defined which used the cubes to carve out the shape of the layer, ensuring that the edges were tapered. There is also a loop utilized in the program that iterates through the specified number of steps (STEPS), each representing a layer of the structure.

The size of each layer decreases gradually, and the rotation angle increases as the loop progresses, resulting in a stepped pyramid-like appearance. 

Through this process, we can create a spiral-looking, structure that allows us to visualize the Fibonacci spiral in a cube format.  Show below is another representation of the same Golden Ratio however in this case, the code generates a series of tapered cubes stacked on top of each other. The size of each cube decreases exponentially as we move upwards 

Shown below is a visual representation of 

We were ready to export this and see the powder printer go, but alas we ran into problems:

However, after running into Prof. Kagey in the Makerspace, we were able to export our files to him, and we should have our prints soon!