For the final project, I wanted to do something with music and math. I listen to a lot of music in my free time and Nora’s second project on Fourier Transforms was really interesting. I decided to use the integer sequences from the Online Encyclopedia of Integer Sequences (OEIS) and try to transform the sounds they generate into longer melodies.

For some context, (OEIS) serves as a comprehensive repository of mathematical sequences, boasting a vast collection of patterns and relationships among integers. From Fibonacci numbers to prime sequences, OEIS offers a wealth of data curated by mathematicians worldwide. However, not all sequences within OEIS lend themselves to musical interpretation. Only a subset of sequences possesses attributes conducive to being translated into playable sounds. These playable sequences often exhibit regularity, periodicity, or rhythmic patterns that can be mapped onto musical notes.

The database does have tags indicating which sequences can be played vs not. By selectively filtering for these sequences and using algorithms to convert them into melodic fragments, we can create melodies with these sequences.

technical process

I started by downloading the online OEIS database which is formatted as follows.

The process begins by harnessing the power of the OEIS API to access specific endpoints designed to identify sequences that are conducive to being played as sounds.

By making calls to these endpoints, we can get a list of playable sequences. Then since, we know the names of these sequences, we can filter through the database pictured above and remove every sequence that does not belong to the list of playable sequences.

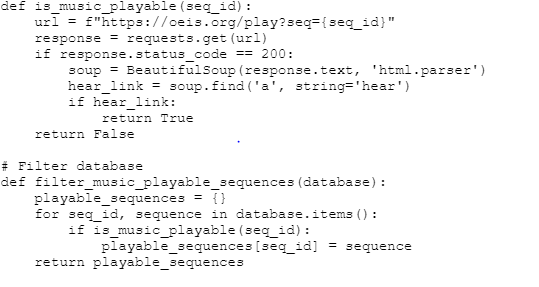
The code above shows how I went about this filtering:

Once the playable sequences are identified, another API call retrieves the actual WAV files associated with each sequence. To seamlessly merge these auditory fragments into cohesive compositions, I used a Python library named moviepy. This library facilitates the conversion of WAV files into MOV files, enabling the manipulation and arrangement of sound sequences.

One thing to note is that when the WAV files convert to MOV files, the length of the files are not consistent with some files being over 15 minutes. For the sake of consistency, I cut each movie file to be the first two seconds.

Finally I randomly assign the sequences next to each other and put them together creating one long MOV file at the end. This is an example of what one MOV file was:

math & music theory

The coolest part about this project was learning about all of the math behind music theory. One specific application would be mapping different notes to modulo arithmetic which allows us to model the cyclical nature of musical scales. For example, by applying modulo arithmetic to the twelve-tone equal temperament system, each note in the scale is represented by a number modulo twelve, allowing for the seamless transition between octaves.

For instance, understanding the concept of a perfect fourth and perfect fifth involves recognizing the intervals between notes as multiples of a certain number of semitones. A perfect fourth spans five semitones, while a perfect fifth spans seven semitones, forming the basis of chord structures and harmonic progressions.

Furthermore, Fourier transforms play a pivotal role in understanding the frequency components of musical sounds. By decomposing complex waveforms into their constituent sinusoidal components, Fourier transforms enable the analysis and synthesis of musical timbres and textures.

This is all very related to how OEIS translates the integer sequences into playable sounds. By assigning numerical values to specific musical notes and durations, and by mapping these values onto the sequences extracted from OEIS, the project transforms abstract mathematical patterns into tangible auditory experiences, demonstrating the connection between mathematics and music.

improving the melodies

When I randomly concatenated the sequences, they sounded disjointed and not very pleasant. I wanted to make these melodies sound more aesthetically pleasing. With all of this music theory in mind, I started to look into chord progressions, melodic contour, and rhythmic patterns.

Drawing upon semitones and modulo arithmetic, I decided to create a modulo 12 map that I could map each integer in the sequence to. I then experimented with different sequence combinations to achieve a more harmonious blend of musical elements.

Unfortunately these sequences sounded the same so I’m debugging the code to see if it’s an implementation issue or if I should attempt it again with a different modulo map.

future steps

Beyond continuing to try and make this sound better, I think one cool expansion could be generating visualizations for sounds. I found a bunch of auditory python libraries that would do different trigonometric graphs for audio that are customizable.

By synchronizing visual representations with the auditory experience, it could be cool to create some sort of immersive multimedia artworks.